BayesMultiMode is an R package for detecting and
exploring multimodality using Bayesian techniques. The approach works in
two stages. First, a mixture distribution is fitted on the data using a
sparse finite mixture Markov chain Monte Carlo (SFM MCMC) algorithm. The
number of mixture components does not have to be known; the size of the
mixture is estimated endogenously through the SFM approach. Second, the
modes of the estimated mixture in each MCMC draw are retrieved using
algorithms specifically tailored for mode detection. These estimates are
then used to construct posterior probabilities for the number of modes,
their locations and uncertainties, providing a powerful tool for mode
inference. See Basturk et al. (2023) and Cross et al. (2024) for more
details.
install.packages("BayesMultiMode")# install.packages("devtools") # if devtools is not installed
devtools::install_github("paullabonne/BayesMultiMode")library(BayesMultiMode)BayesMultiMode provides a very flexible and efficient
MCMC estimation approach : it handles mixtures with unknown number of
components through the sparse finite mixture approach of Malsiner-Walli,
Fruhwirth-Schnatter, and Grun (2016) and supports a comprehensive range
of mixture distributions, both continuous and discrete.
set.seed(123)
# retrieve galaxy data
y = galaxy
# estimation
bayesmix = bayes_fit(data = y,
K = 10,
dist = "normal",
nb_iter = 2000,
burnin = 1000,
print = F)
plot(bayesmix, draws = 200)
# mode estimation
bayesmode = bayes_mode(bayesmix)
plot(bayesmode)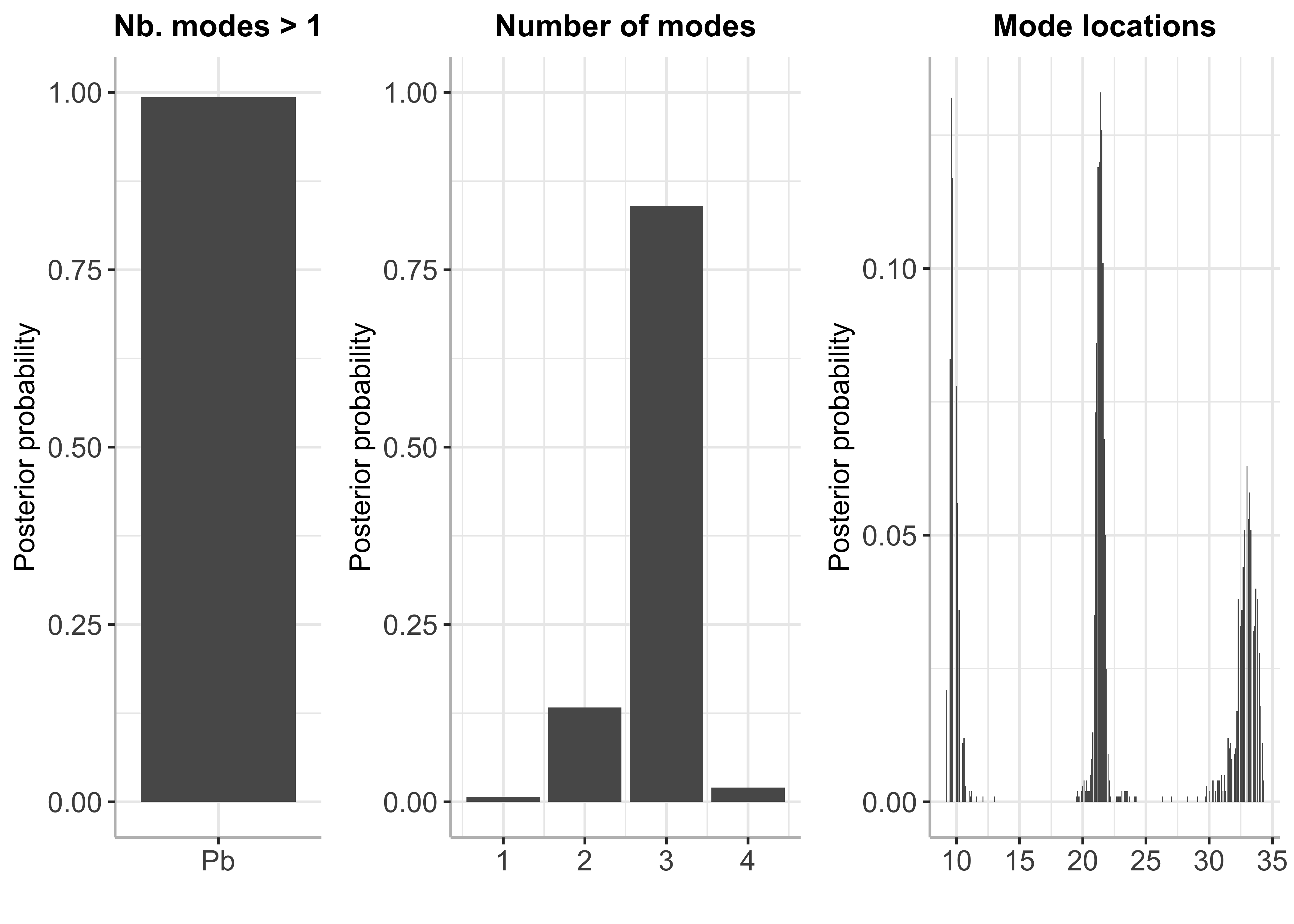
summary(bayesmode)## Posterior probability of multimodality is 0.993
##
## Inference results on the number of modes:
## p_nb_modes (matrix, dim 4x2):
## number of modes posterior probability
## [1,] 1 0.007
## [2,] 2 0.133
## [3,] 3 0.840
## [4,] 4 0.020
##
## Inference results on mode locations:
## p_loc (matrix, dim 252x2):
## mode location posterior probability
## [1,] 9.2 0.021
## [2,] 9.3 0.000
## [3,] 9.4 0.000
## [4,] 9.5 0.083
## [5,] 9.6 0.132
## [6,] 9.7 0.117
## ... (246 more rows)BayesMultiMode also works on MCMC output generated using
external software. The function bayes_mixture() creates an
object of class bayes_mixture which can then be used as
input in the mode inference function bayes_mode(). Here is
an example using cyclone intensity data (Knapp et al. 2018) and the
BNPmix package for estimation. More examples can be found
here.
library(BNPmix)
library(dplyr)
y = cyclone %>%
filter(BASIN == "SI",
SEASON > "1981") %>%
dplyr::select(max_wind) %>%
unlist()
## estimation
PY_result = PYdensity(y,
mcmc = list(niter = 2000,
nburn = 1000,
print_message = FALSE),
output = list(out_param = TRUE))mcmc_py = list()
for (i in 1:length(PY_result$p)) {
k = length(PY_result$p[[i]][, 1])
draw = c(PY_result$p[[i]][, 1],
PY_result$mean[[i]][, 1],
sqrt(PY_result$sigma2[[i]][, 1]),
i)
names(draw)[1:k] = paste0("eta", 1:k)
names(draw)[(k+1):(2*k)] = paste0("mu", 1:k)
names(draw)[(2*k+1):(3*k)] = paste0("sigma", 1:k)
names(draw)[3*k + 1] = "draw"
mcmc_py[[i]] = draw
}
mcmc_py = as.matrix(bind_rows(mcmc_py))bayes_mixturepy_BayesMix = bayes_mixture(mcmc = mcmc_py,
data = y,
burnin = 0, # the burnin has already been discarded
dist = "normal",
vars_to_keep = c("eta", "mu", "sigma"))plot(py_BayesMix)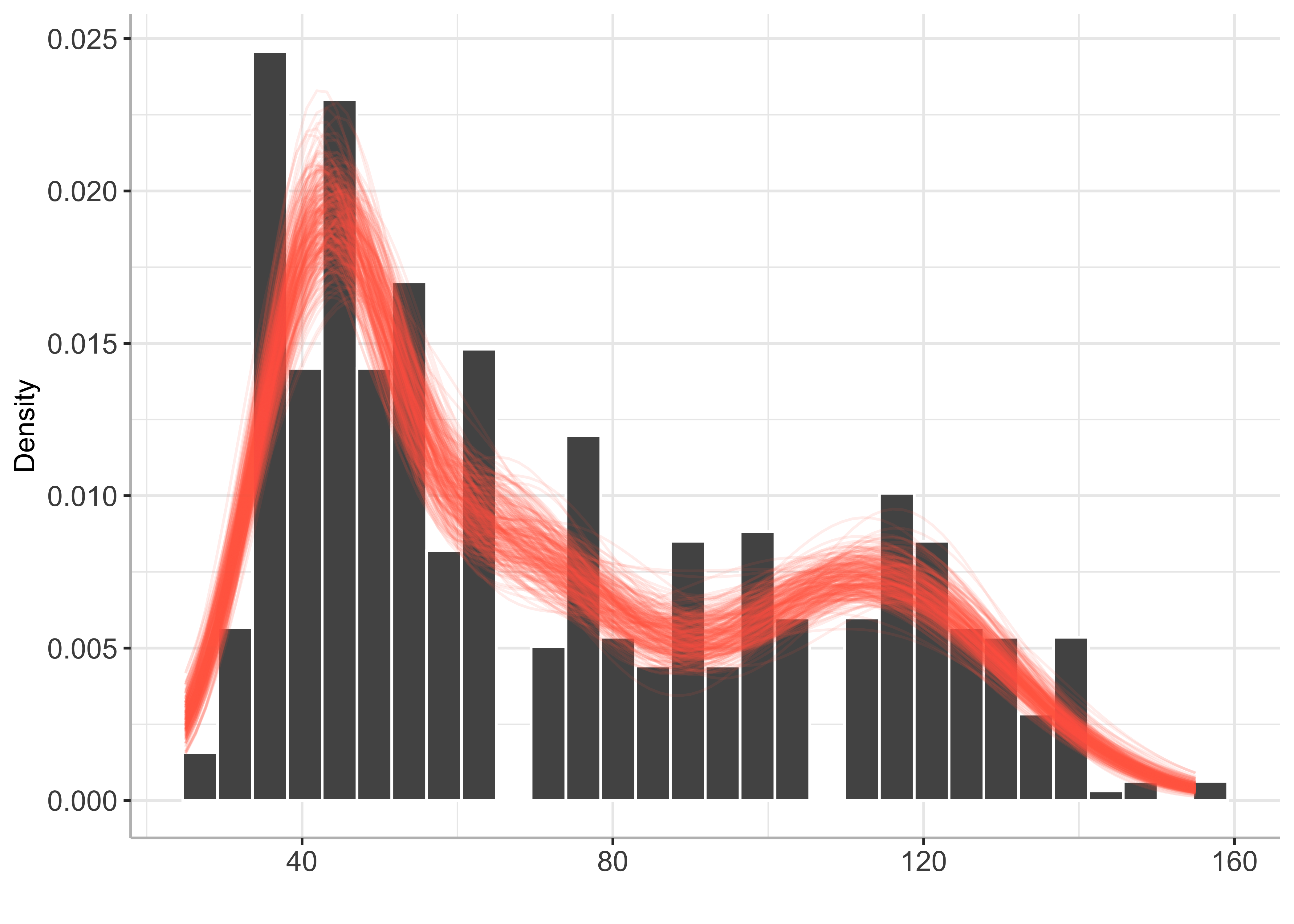
# mode estimation
bayesmode = bayes_mode(py_BayesMix)
# plot
plot(bayesmode)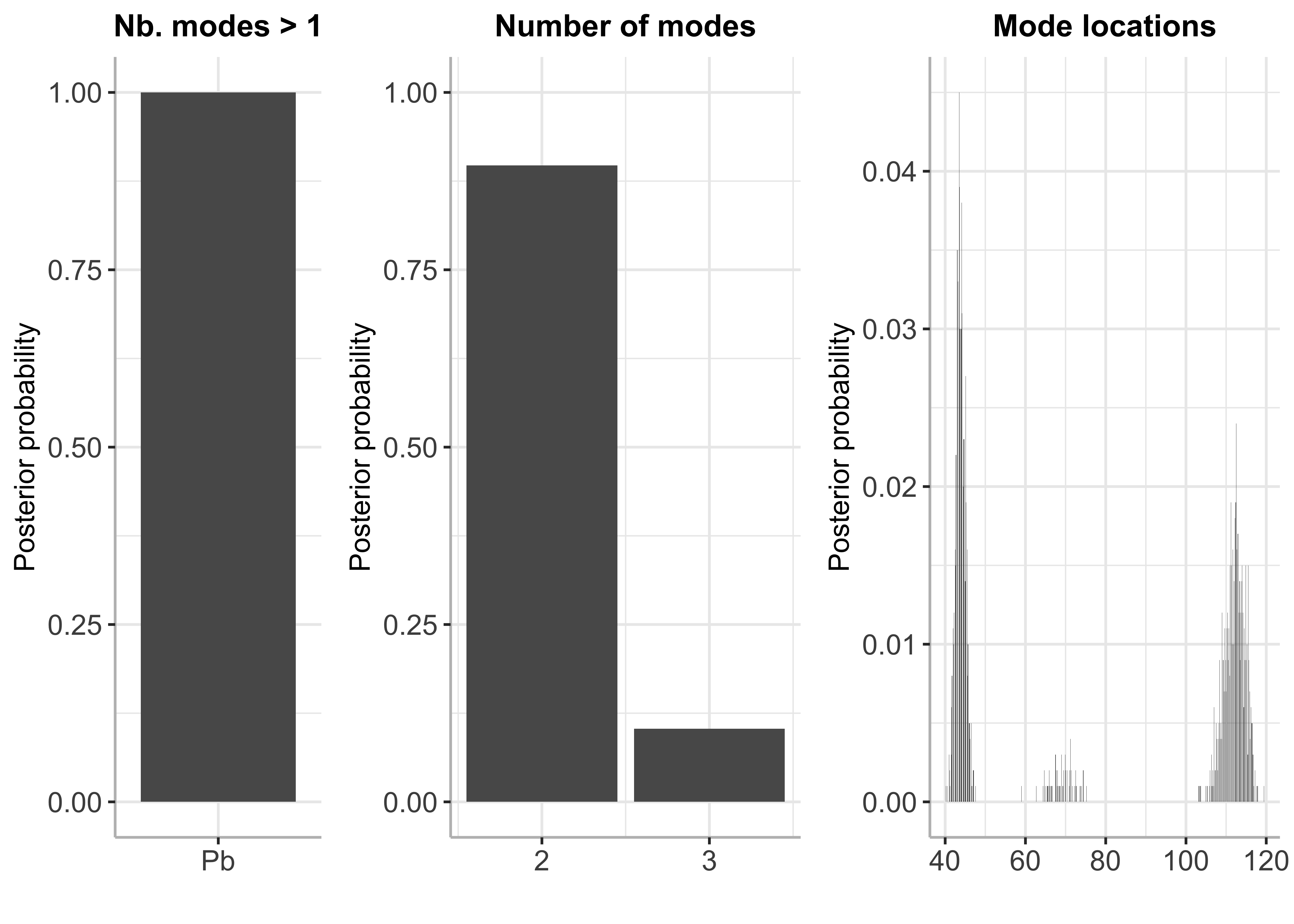
# Summary
summary(bayesmode)## Posterior probability of multimodality is 1
##
## Inference results on the number of modes:
## p_nb_modes (matrix, dim 2x2):
## number of modes posterior probability
## [1,] 2 0.897
## [2,] 3 0.103
##
## Inference results on mode locations:
## p_loc (matrix, dim 793x2):
## mode location posterior probability
## [1,] 40.2 0.001
## [2,] 40.3 0.000
## [3,] 40.4 0.000
## [4,] 40.5 0.001
## [5,] 40.6 0.000
## [6,] 40.7 0.000
## ... (787 more rows)It is possible to use BayesMultiMode to find modes in
mixtures estimated using maximum likelihood and the EM algorithm. Below
is an example using the popular package mclust. More
examples can be found here.
set.seed(123)
library(mclust)
y = cyclone %>%
filter(BASIN == "SI",
SEASON > "1981") %>%
dplyr::select(max_wind) %>%
unlist()
fit = Mclust(y)
pars = c(eta = fit$parameters$pro,
mu = fit$parameters$mean,
sigma = sqrt(fit$parameters$variance$sigmasq))
mix = mixture(pars, dist = "normal", range = c(min(y), max(y))) # create new object of class Mixture
modes = mix_mode(mix) # estimate modes
plot(modes)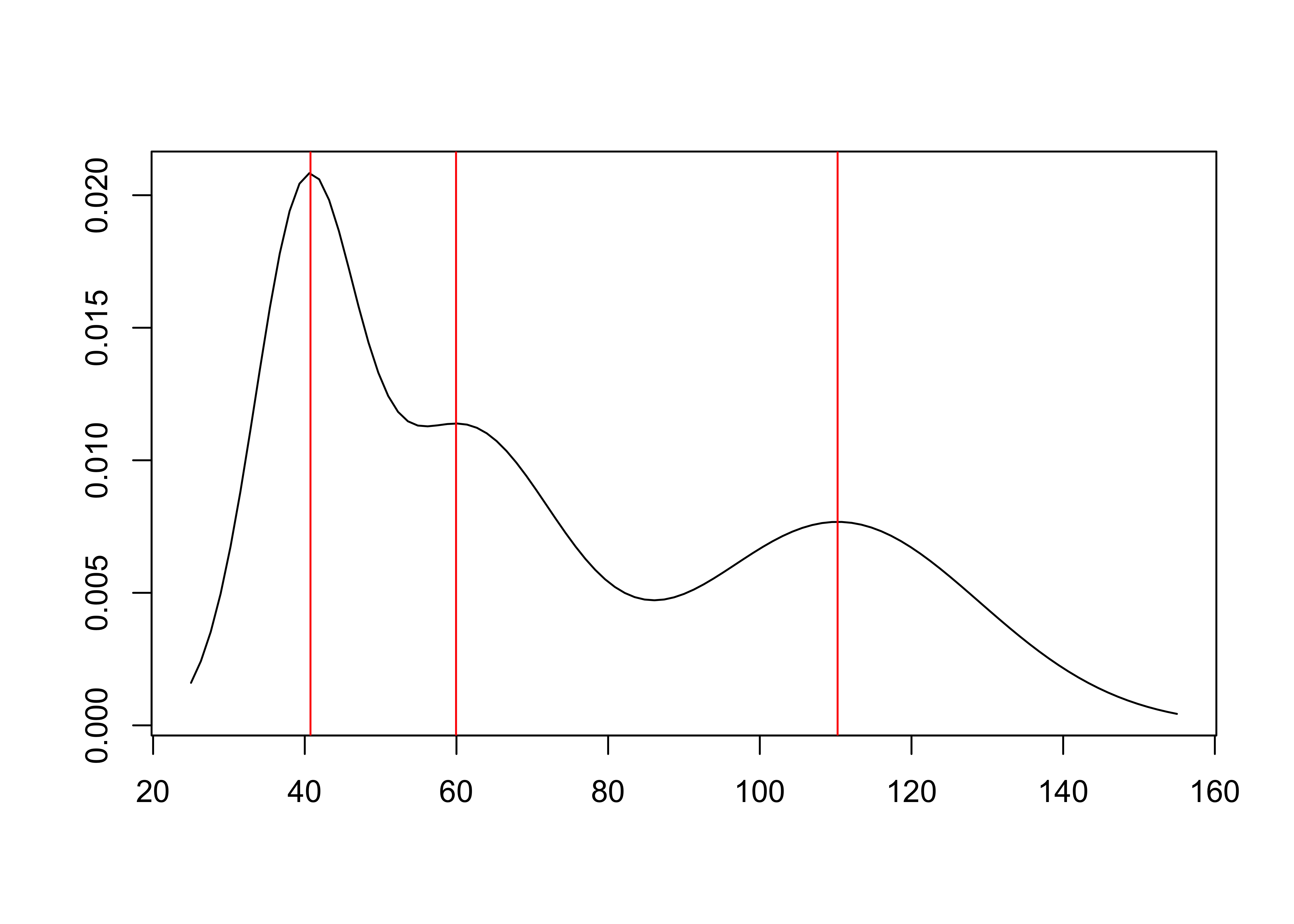
summary(modes)## Modes of a normal mixture with 3 components.
## - Number of modes found: 3
## - Mode estimation technique: fixed-point algorithm
## - Estimates of mode locations:
## mode_estimates (numeric vector, dim 3):
## [1] 41 60 110