Package: hypergeo2
0.2.0
Author: Xiurui Zhu
Modified: 2024-09-17 23:33:00
Compiled: 2024-10-14 22:55:54
The goal of hypergeo2 is to implement generalized
hypergeometric function with tunable high precision. Two floating-point
datatypes – mpfr_float and gmp_float – are
channeled into this package. The computation is limited to real numbers,
since its underlying workhorse boost::math::detail::hypergeometric_pFq_checked_series()
from BH
package implements comparisons (> or
<) between numbers, which are not defined for complex
datatypes.
If you are building from source (e.g. not installing binaries on Windows), you need to prepare for two system requirements: ‘gmp’ and ‘mpfr’, to facilitate high-precision floating point types. You may follow the installation instructions from their websites, or try the following commands for quick (default) installation.
pacman -Syu make pkg-config libtool gmp mpfrbrew install gmp mpfrconfigure file, or install them using
conda.If you are running R from an isolated environment
(e.g. conda), you need to first activate the environment,
and then build the system requirements and the package in the same
environment to avoid version conflicts such as: undefined reference to
memcpy@GLIBC#.#.#.
If the requirements are installed into their default paths
(e.g. without using the --prefix option), you are OK to go
ahead installing the package in R, as pkg-config will take
care finding them.
You can install the released version of hypergeo2 from
CRAN with:
install.packages("hypergeo2")Alternatively, you can install the developmental version of
hypergeo2 from github
with:
remotes::install_github("zhuxr11/hypergeo2")However, if the requirements are not installed into their default
paths, you may first need to provide configuration arguments/variables
to installation paths. Optionally, you may also designate the maximal
series iteration, default at 10000. To sum up, you may configure the
installation in one of the following ways (replacing
<my_gmp_install>,
<my_mpfr_install> and
<my_max_iter> with your paths) before installing the
package with R CMD INSTALL in bash:
--configure-args in
R CMD INSTALL:MY_GMP_INSTALL='<my_gmp_install>'
MY_MPFR_INSTALL='<my_mpfr_install>'
MY_MAX_ITER=<my_max_iter>
R CMD INSTALL hypergeo2 \
--configure-args="\
--with-gmp-include=${MY_GMP_INSTALL}/include \
--with-mpfr-include=${MY_MPFR_INSTALL}/include \
--with-gmp-lib=${MY_GMP_INSTALL}/lib \
--with-mpfr-lib=${MY_MPFR_INSTALL}/lib \
--with-max-iter=${MY_MAX_ITER}\
"--configure-vars in
R CMD INSTALL:MY_GMP_INSTALL='<my_gmp_install>'
MY_MPFR_INSTALL='<my_mpfr_install>'
MY_MAX_ITER=<my_max_iter>
R CMD INSTALL hypergeo2 \
--configure-vars="\
GMP_INCLUDE=${MY_GMP_INSTALL}/include \
MPFR_INCLUDE=${MY_MPFR_INSTALL}/include \
GMP_LIB=${MY_GMP_INSTALL}/lib \
MPFR_LIB=${MY_MPFR_INSTALL}/lib \
MAX_ITER=${MY_MAX_ITER}\
"Sometimes, computing generalized hypergeometric function in double
precision is not sufficient, even though we only need 6-8 accurate
digits in the results. Here, two floating-point datatypes are provided:
mpfr_float (“mpfr”) and gmp_float (“gmp”). By
comparison, the “mpfr” backend is safer, since it defines while the
“gmp” backend throws overflow exception. Therefore,
mpfr_float is used as the default backend.
library(hypergeo2)For example, let us compute a generalized hypergeometric function in Matlab Online and use its value as reference:
>> fprintf("%.32g", hypergeom([-28.2 11.8 15.8], [12.8 17.8], 1))
2.7120446907792120783054486094854e-09First, we compute the same function with
hypergeo::genhypergeo() function.
hypergeo_U <- c(-28.2, 11.8, 15.8)
hypergeo_L <- c(12.8, 17.8)
hypergeo_z <- 1
(hypergeo_res <- hypergeo::genhypergeo(U = hypergeo_U, L = hypergeo_L, z = hypergeo_z))
#> [1] 3.419707e-09As can be seen, the result is heavily deviated by 0.261 in terms of relative error.
Then, we compute the same function with
hypergeo2::genhypergeo() function, at default (double)
precision.
(hypergeo2_res_double <- genhypergeo(U = hypergeo_U, L = hypergeo_L, z = hypergeo_z))
#> [1] 2.781375e-09As can be seen, the result is still deviated by 0.0256 in terms of relative error, although much better.
Next, we compute the same function with
hypergeo2::genhypergeo() function, with a precision of 20
digits from mpfr and gmp backends,
respectively.
(hypergeo2_res_prec20_mpfr <- genhypergeo(U = hypergeo_U, L = hypergeo_L, z = hypergeo_z,
prec = 20L, backend = "mpfr"))
#> [1] 2.712035e-09
(hypergeo2_res_prec20_gmp <- genhypergeo(U = hypergeo_U, L = hypergeo_L, z = hypergeo_z,
prec = 20L, backend = "gmp"))
#> [1] 2.712045e-09As can be seen, the result from gmp backend is more
precise than that from mpfr, with the deviation of
mpfr at -3.75e-06 and that of gmp at 2.68e-09.
This is because that gmp usually use higher precision than
we set (see this
post).
Finally, to validate this hypothesis, we further increase the precision to 25 digits.
(hypergeo2_res_prec25_mpfr <- genhypergeo(U = hypergeo_U, L = hypergeo_L, z = hypergeo_z,
prec = 25L, backend = "mpfr"))
#> [1] 2.712045e-09
(hypergeo2_res_prec25_gmp <- genhypergeo(U = hypergeo_U, L = hypergeo_L, z = hypergeo_z,
prec = 25L, backend = "gmp"))
#> [1] 2.712045e-09As can be seen, now both results are very close to the reference,
with deviations from mpfr and gmp backends at
2.72e-09 and 2.68e-09, respectively.
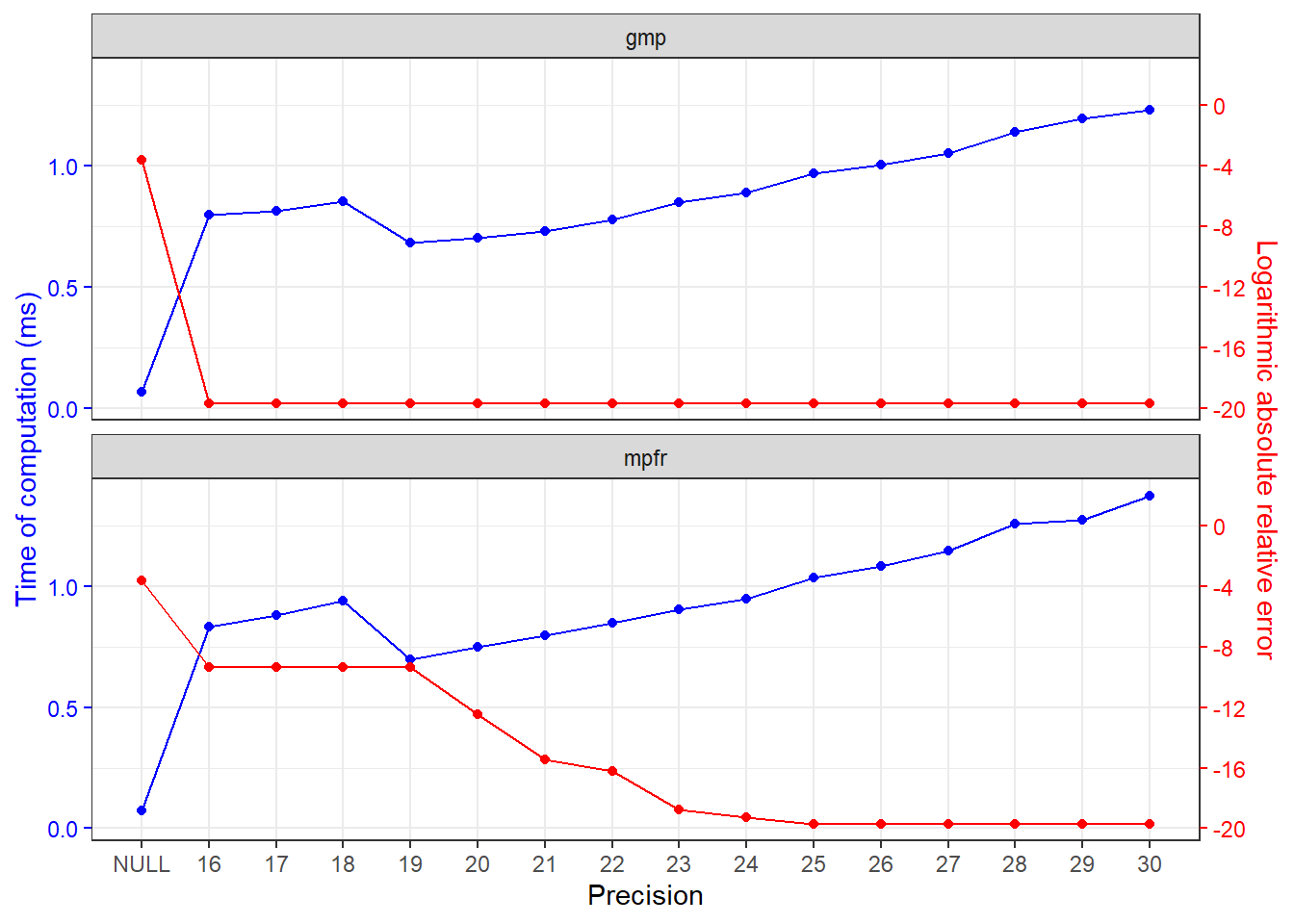
The time of computation at different precision is profiled in this section.
bench_scheme <- expand.grid(prec = c(list(NULL), as.list(seq(16L, 30L))),
backend = c("mpfr", "gmp"),
stringsAsFactors = FALSE)
bench_fun <- function(prec, backend, quote = FALSE) {
res <- bquote(genhypergeo(U = hypergeo_U, L = hypergeo_L, z = hypergeo_z,
prec = .(prec), backend = .(backend)) / ref_value - 1)
if (quote == FALSE) {
eval(res)
} else {
res
}
}
bench_scheme[["err"]] <- mapply(
FUN = bench_fun,
prec = bench_scheme[["prec"]],
backend = bench_scheme[["backend"]],
USE.NAMES = FALSE,
SIMPLIFY = TRUE
)
bench_res <- summary(microbenchmark::microbenchmark(
list = mapply(
FUN = bench_fun,
prec = bench_scheme[["prec"]],
backend = bench_scheme[["backend"]],
MoreArgs = list(quote = TRUE),
USE.NAMES = FALSE,
SIMPLIFY = TRUE
),
times = 100L
))
bench_res <- cbind(bench_scheme, bench_res[colnames(bench_res) %in% "expr" == FALSE])
bench_res[["prec"]] <- as.character(bench_res[["prec"]])
ggplot2::ggplot(
bench_res,
ggplot2::aes(x = as.integer(factor(prec, levels = unique(prec))))
) +
ggplot2::geom_point(ggplot2::aes(y = mean / 1000), color = "blue") +
ggplot2::geom_line(ggplot2::aes(y = mean / 1000), color = "blue") +
ggplot2::geom_point(ggplot2::aes(y = (log(abs(err)) + 20) / 16), color = "red") +
ggplot2::geom_line(ggplot2::aes(y = (log(abs(err)) + 20) / 16), color = "red") +
ggplot2::scale_x_continuous(breaks = seq_along(unique(bench_res[["prec"]])),
minor_breaks = NULL,
labels = unique(bench_res[["prec"]])) +
ggplot2::scale_y_continuous(
sec.axis = ggplot2::sec_axis(~. * 16 - 20,
breaks = seq(-20, 0, by = 4),
name = "Logarithmic absolute relative error")
) +
ggplot2::facet_wrap(ggplot2::vars(backend), ncol = 1L) +
ggplot2::theme_bw() +
ggplot2::theme(
axis.title.y.left = ggplot2::element_text(color = "blue"),
axis.text.y.left = ggplot2::element_text(color = "blue"),
axis.ticks.y.left = ggplot2::element_line(color = "blue"),
axis.title.y.right = ggplot2::element_text(color = "red"),
axis.text.y.right = ggplot2::element_text(color = "red"),
axis.ticks.y.right = ggplot2::element_line(color = "red")
) +
ggplot2::labs(x = "Precision", y = "Time of computation (ms)")