

The latent2likert package is designed to effectively simulate the discretization process inherent to Likert scales while minimizing distortion. It converts continuous latent variables into ordinal categories to generate Likert scale item responses. This is particularly useful for accurately modeling and analyzing survey data that use Likert scales, especially when applying statistical techniques that require metric data.
You can install the development version from GitHub with:
# install.packages("devtools")
devtools::install_github("markolalovic/latent2likert")To keep the package lightweight, latent2likert only imports mvtnorm, along with the standard R packages stats and graphics, which are typically included in R releases. An additional suggested dependency is the package sn, which is required only for generating random responses from correlated Likert items based on a multivariate skew normal distribution. The package prompts the user to install this dependency during interactive sessions if needed.
rlikert: Generates random responses to Likert scale
questions based on specified means and standard deviations of latent
variables, with optional settings for skewness and correlations.estimate_params: Estimates latent parameters from
existing survey data.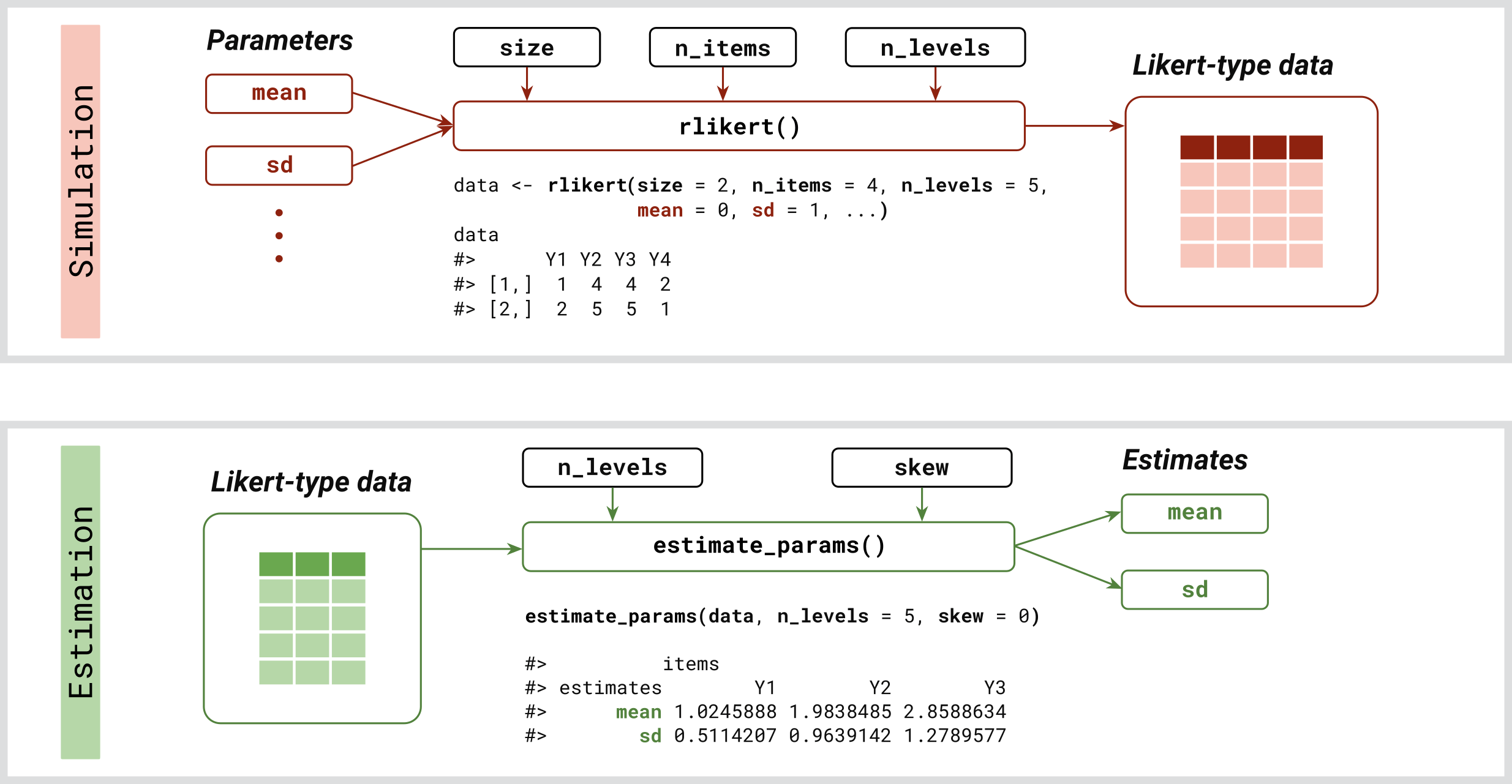
rlikertTo generate a sample of random responses to one item on a 5-point Likert scale, use:
library(latent2likert)
rlikert(size = 10, n_items = 1, n_levels = 5)
#> [1] 1 2 5 5 2 3 4 2 4 4To generate responses to multiple items with specified parameters:
rlikert(size = 10,
n_items = 3,
n_levels = c(4, 5, 6),
mean = c(0, -1, 0),
sd = c(0.8, 1, 1),
corr = 0.5)
#> Y1 Y2 Y3
#> [1,] 3 4 5
#> [2,] 3 2 4
#> [3,] 2 1 2
#> [4,] 4 3 6
#> [5,] 3 3 4
#> [6,] 4 3 6
#> [7,] 2 1 1
#> [8,] 3 4 4
#> [9,] 2 3 4
#> [10,] 2 1 4You can also provide a correlation matrix:
corr <- matrix(c(1.00, -0.63, -0.39,
-0.63, 1.00, 0.41,
-0.39, 0.41, 1.00), nrow=3)
data <- rlikert(size = 10^3,
n_items = 3,
n_levels = c(4, 5, 6),
mean = c(0, -1, 0),
sd = c(0.8, 1, 1),
corr = corr)Note that the correlations among the Likert response variables are only estimates of the actual correlations between the latent variables, and these estimates are typically lower:
cor(data)
#> Y1 Y2 Y3
#> Y1 1.0000000 -0.5452650 -0.3539568
#> Y2 -0.5452650 1.0000000 0.3084354
#> Y3 -0.3539568 0.3084354 1.0000000estimate_paramsGiven the data, you can estimate the values of latent parameters using:
estimate_params(data, n_levels = c(4, 5, 6), skew = 0)
#> items
#> estimates Y1 Y2 Y3
#> mean 0.04691194 -1.01865288 0.01471470
#> sd 0.77732152 0.96811355 1.01830061To visualize the transformation, you can use
plot_likert_transform(). It plots the densities of latent
variables in the first row and transformed discrete probability
distributions below:
plot_likert_transform(n_items = 3,
n_levels = 5,
mean = c(0, -1, 0),
sd = c(0.8, 1, 1),
skew = c(0, 0, 0.5))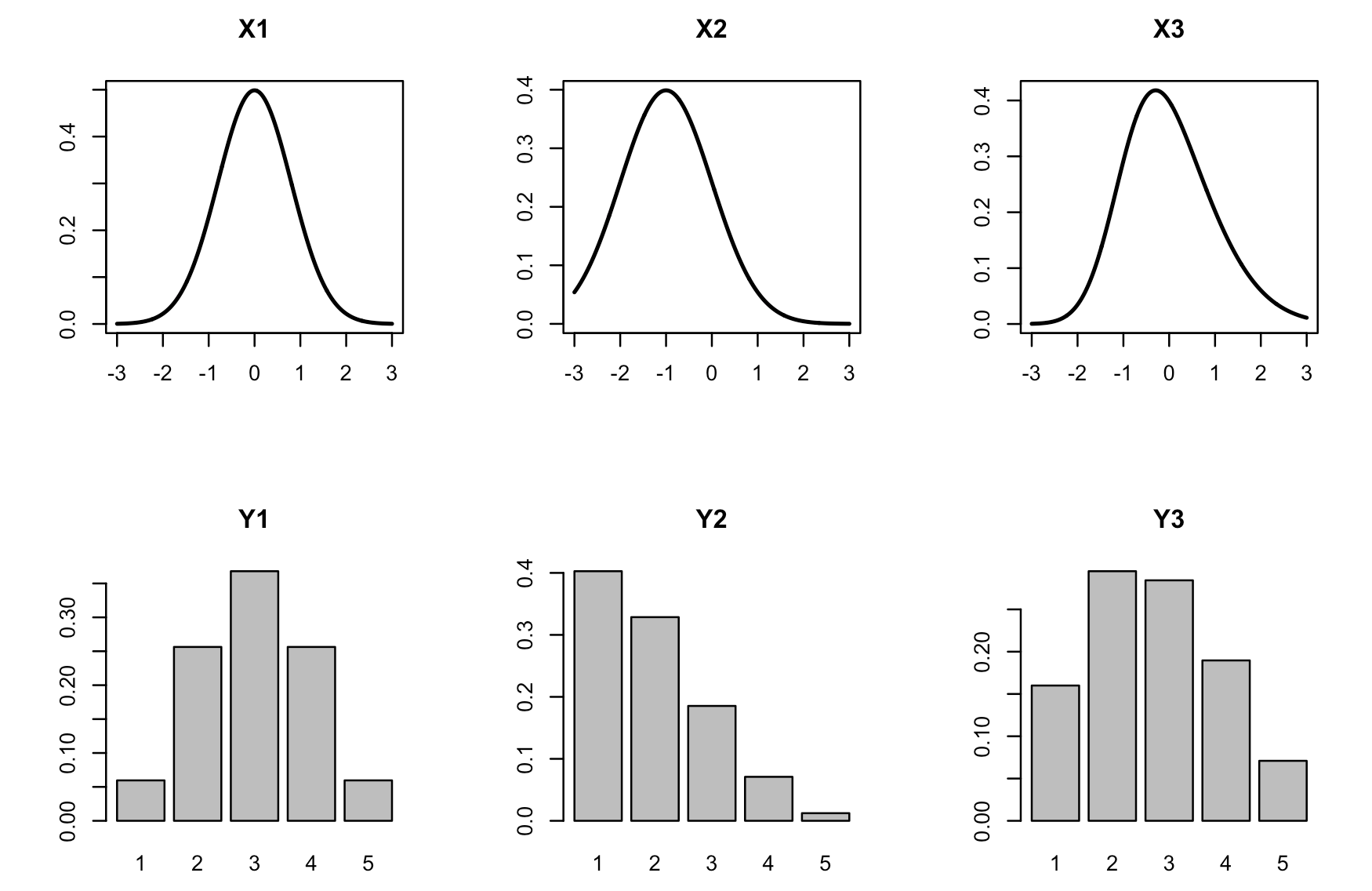
Note that, depending on the value of the skewness parameter, the normal latent distribution is used if skew = 0, otherwise the skew normal distribution is used. The value of skewness is restricted to the range -0.95 to 0.95, that is
skew >= -0.95andskew <= 0.95.
To simulate Likert item responses, the draw_likert
function from the fabricatr
package can be used to recode a latent variable into a Likert response
variable by specifying intervals that subdivide the continuous range.
The latent2likert package, however, offers an advantage
by automatically calculating optimal intervals that minimize distortion
between the latent variable and the Likert response variable for both
normal and skew normal latent distributions, eliminating the need to
manually specify the intervals.
There are also several alternative approaches that do not rely on
latent distributions. One method involves directly defining a discrete
probability distribution and sampling from it using the
sample function in R or the likert function
from the wakefield
package. Another approach is to specify the means, standard deviations,
and correlations among Likert response variables. For this, you can use
LikertMakeR
or SimCorMultRes
to generate correlated multinomial responses.
Additionally, you can define a data generating process. For those familiar with item response theory, the mirt package allows users to specify discrimination and difficulty parameters for each response category.